CRP Tutorial
Single-trial example
We will label presented items (for our lab, usually words) with numbers 1-8, in sequence, so our hypothetical participant sees this string of items, one at a time:
1 2 3 4 5 6 7 8
The participant is told to recall the presented items in any order, and then recalls items corresponding to the following numbers, in this order:
8 7 1 2 3 5 6 4
Let's first tally up the transitions that were actually made:
- 8 to 7: lag of -1
- 7 to 1: lag of -6
- 1 to 2: lag of +1
- 2 to 3: lag of +1
- 3 to 5: lag of +2
- 5 to 6: lag of +1
- 6 to 4: lag of -2
This gives us an actual transition tally that looks like this:
| Lag | -7 | -6 | -5 | -4 | -3 | -2 | -1 | +1 | +2 | +3 | +4 | +5 | +6 | +7 |
| Actual count | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |
Note that the maximum absolute lag possible with a list of 8 items is 8-1=7 (i.e., a transition from first to last or vice versa).
Because we want a conditional response probability, we also have to tally up the transitions that could have been made at each output. The list is long, so please click "Expand" below to show:
Possible transitions
- After the first output (item 8), the participant could have recalled:
- Item 1: lag of -7
- Item 2: lag of -6
- Item 3: lag of -5
- Item 4: lag of -4
- Item 5: lag of -3
- Item 6: lag of -2
- Item 7: lag of -1
- After the second output (item 7), the participant could have recalled:
- Item 1: lag of -6
- Item 2: lag of -5
- Item 3: lag of -4
- Item 4: lag of -3
- Item 5: lag of -2
- Item 6: lag of -1
- Note that the participant can not make a valid transition of +1, since item 8 has already been recalled
- After the third output (item 1), the participant could have recalled:
- Item 2: lag of +1
- Item 3: lag of +2
- Item 4: lag of +3
- Item 5: lag of +4
- Item 6: lag of +5
- Note that the participant can not make valid transitions of +6 or +7, since items 7 and 8 have already been recalled
- After the fourth output (item 2), the participant could have recalled:
- Item 3: lag of +1
- Item 4: lag of +2
- Item 5: lag of +3
- Item 6: lag of +4
- Note that the participant can not make valid transitions of -1, +5 or +6, since items 1, 7 and 8 have already been recalled
- After the fifth output (item 3), the participant could have recalled:
- Item 4: lag of +1
- Item 5: lag of +2
- Item 6: lag of +3
- Note that the participant can not make valid transitions of -1, -2, +4 or +5, since items 1, 2, 7 and 8 have already been recalled
- After the sixth output (item 5), the participant could have recalled:
- Item 4: lag of -1
- Item 6: lag of +1
- Note that the participant can not make valid transitions of -4, -3, -2, +2 or +3, since items 1, 2, 3, 7 and 8 have already been recalled
- After the seventh output (item 6), the participant could only have validly recalled:
- Item 4: lag of -2
- Note that this is the only valid transition left, since all other items have been recalled.
- After the eighth output (item 4), there are no more possible valid transitions
- Note that repetitions are never included, since they do not count as valid transitions.
Adding up all possible lags, we get a possible transition tally of:
| Lag | -7 | -6 | -5 | -4 | -3 | -2 | -1 | +1 | +2 | +3 | +4 | +5 | +6 | +7 |
| Possible count | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 3 | 3 | 2 | 1 | 0 | 0 |
We then divide the actual count by the possible count to get the conditional probability:
| Lag | -7 | -6 | -5 | -4 | -3 | -2 | -1 | +1 | +2 | +3 | +4 | +5 | +6 | +7 |
| Actual count | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |
| Possible count | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 3 | 3 | 2 | 1 | 0 | 0 |
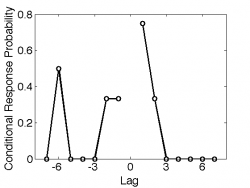
| Conditional Probability | 0 | 0.50 | 0 | 0 | 0 | 0.33 | 0.33 | 0.75 | 0.33 | 0 | 0 | 0 | 0 | 0 |
This makes an extremely noisy lag-CRP curve (right), but this is expected with (a) such a short list, and especially (b) only a single trial.
Multi-trial example
This example is more advanced and assumes some programming knowledge, ideally in Matlab. (Ports of the examples to other languages are coming soon.)
The subject here is presented with X lists. In the below pres matrix, each row is a trial and each column is a serial position. The numbers are identifiers for the word that was presented (out of a 1638-item wordpool). For example, in the first trial, the subject was presented with word 1062, then 219, then 779, and so on. There are 16 columns, so the subject was presented with 16 items in each trial.
You may copy and paste the below code block into Matlab to create the pres variable.
pres = [1062 219 779 148 668 1458 694 1637 475 1433 912 1416 785 1411 701 969; 1175 788 653 1031 1410 184 1134 993 152 313 1033 1591 652 1115 1184 1531; 329 605 414 1614 852 950 1105 10 1144 459 856 455 1178 277 1415 1118; 843 1173 1067 46 1435 1561 1202 30 270 493 815 102 233 796 500 753; 1044 372 556 1600 685 1598 409 989 1326 100 757 94 1491 1398 56 1261; 257 1454 315 1596 1400 1578 840 1069 1294 1254 572 758 1052 620 1230 380; 546 811 252 1093 147 241 589 1351 1373 1446 1621 310 920 188 22 339; 1179 1402 1468 581 1629 647 710 207 1313 1627 378 397 400 515 1579 1038; 1107 410 206 1413 441 930 1439 975 242 109 1257 1193 535 1471 122 132; 1427 555 949 1204 116 540 479 582 1386 888 258 1342 1198 574 87 1008];
After presentation of each list, the subject is given a period to recall the presented items in any order. In the below rec matrix, each row is a recall period following the corresponding presentations from the pres matrix. For example, in the recall period following the first trial's presented items, the subject recalled item 701, then 969, then 475, and so on. There are varying numbers of non-zero entries per row, indicating that the subject recalled a different number of items from the corresponding list in each trial, for example, 7 in the first trial, 5 in the second, and so on.
Zeros are placeholders indicating no recall. (The subject was given a fixed 75 second recall period to recall as many words as possible.)
You may copy and paste the below code block into Matlab to create the rec variable.
rec = [ 701 969 475 785 1411 1062 219 0 0 0 0 0 0 0 0 0; 1531 313 1033 993 1134 0 0 0 0 0 0 0 0 0 0 0; 605 414 950 852 277 1415 329 455 1591 0 0 0 0 0 0 0; 500 753 843 1173 46 815 0 0 0 0 0 0 0 0 0 0; 1261 1491 409 989 1044 372 556 1598 757 0 0 0 0 0 0 0; 380 620 1052 315 1596 572 1294 758 1254 0 0 0 0 0 0 0; 339 22 188 1373 1446 589 0 0 0 0 0 0 0 0 0 0; 1038 515 1579 378 0 0 0 0 0 0 0 0 0 0 0 0; 132 1471 1107 1193 1257 410 535 109 1439 930 0 0 0 0 0 0; 87 1342 1008 574 1471 888 479 540 87 116 0 0 0 0 0 0];
The easiest way to construct a lag CRP is from a recalls matrix, which shows the serial position of recalled words. The simplest way to do that is to loop over trials/lists:
nList = size(pres,1); % Number of lists/trials; equal to number of rows in "pres"
listLength = size(pres,2); % Number of presented items per list;
% equal to number of columns in "pres"
recalls = nan(nList,listLength); % Preallocate with NaNs for speed
for i = 1:10 % Loop over trials
[~,recalls(i,:)] = ismember(rec(i,:),pres(i,:)); % Find each recalled item in the
% presented list and report its
% (serial) position
end
recalls % Print the "recalls" matrix to the command windowWhich should produce the following output:
recalls =
15 16 9 13 14 1 2 0 0 0 0 0 0 0 0 0
16 10 11 8 7 0 0 0 0 0 0 0 0 0 0 0
2 3 6 5 14 15 1 12 0 0 0 0 0 0 0 0
15 16 1 2 4 11 0 0 0 0 0 0 0 0 0 0
16 13 7 8 1 2 3 6 11 0 0 0 0 0 0 0
16 14 13 3 4 11 9 12 10 0 0 0 0 0 0 0
16 15 14 9 10 7 0 0 0 0 0 0 0 0 0 0
16 14 15 11 0 0 0 0 0 0 0 0 0 0 0 0
16 14 1 12 11 2 13 10 7 6 0 0 0 0 0 0
15 12 16 14 0 10 7 6 15 5 0 0 0 0 0 0
Remember that the recalls matrix shows the serial position (i.e., position in the presentation list) of each item recalled. For example, in the recall period of the first trial, the subject recalled the item presented in the 15th position, then the 16th position, then the 9th position, and so on.
Zeros indicate either no word recalled, or an intrusion (see point 1 below).
Note two important things:
- Intrusions (recalls that were not presented in the just-seen list) are not included in the recalls matrix above. For example, notice in the third row (i.e., third trial) of rec matrix that the last item recalled is 1591. Word 1591 was presented in trial 2, not trial 3; this is an example of a prior-list intrusion. The corresponding spot in the recalls matrix is zero, because word 1591 was not found in the 3rd row of pres.
- For the purposes of constructing a lag CRP, we can -- and should -- ignore all intrusions, so this is ok.
- In-list repetitions are not noted and show up in the recalls matrix normally. Notice that in the last trial, word 87 is recalled twice, so serial position 15 appears twice in the last row of the recalls matrix. We will have to take care of that before calculating the lag CRP.
Click here for the Software page.